
Movimiento sinusoidal
Cálculo de cilindros hidráulicos, cilindros de oscilación
La oscilación sinusoidal armónica más simple de un eje de cilindro regulado es una entrada y salida cíclica del vástago. Pero también los perfiles de recorrido completamente irregulares pueden describirse matemáticamente asumiendo un movimiento sinusoidal en cada punto.
El cálculo simplificado integrado en el configurador de productos HäKo (cilindro de prueba >> Diseño hidráulico) sirve para el diseño de un movimiento dinámico en funcionamiento sinusoidal. Para ello, se tienen en cuenta sobre todo los datos del cilindro, pero no se incluyen otras piezas relevantes para el sistema, como por ejemplo mangueras o válvulas y sus fugas.
El movimiento sinusoidal se define introduciendo la amplitud y la frecuencia. Con esto, el cálculo determina los valores máximos respectivos del movimiento, que, sin embargo, no se producen simultáneamente en una oscilación sinusoidal. Por ejemplo, la velocidad tiene su valor máximo en el momento en que el valor de la aceleración es cero.
Para determinar el tamaño del cilindro, esto es suficiente para un diseño típico.
Este cálculo no sustituye la simulación del sistema hidráulico completo, que es necesaria en casos especiales, por ejemplo, cuando el sistema llega a sus límites de diseño.
El cálculo sirve para el diseño de un movimiento en funcionamiento sinusoidal. No incluye el comportamiento al conectar o desconectar el sistema hidráulico.
Cálculo de fuerzas
La fuerza del cilindro Fb a la presión de trabajo es la fuerza que se alcanza en el funcionamiento dinámico. La presión de trabajo se refiere a la presión pb que realmente prevalece en la cámara del cilindro y que se ajusta detrás de la válvula de regulación, válvula porporcional.
Fb = pb • A
con la superficie efectiva del pistón a partir del diámetro del pistón D2K y el diámetro de vástago de émbolo d2s
A = π / 4 • (D2K - d2s)
La fuerza del cilindro Fs a la presión del sistema es la fuerza que se alcanza en el funcionamiento estático. La presión del sistema se refiere a la presión ps que prevalece delante de la válvula de regulación, válvula porporcional y que el grupo proporciona.
Fs = ps • A
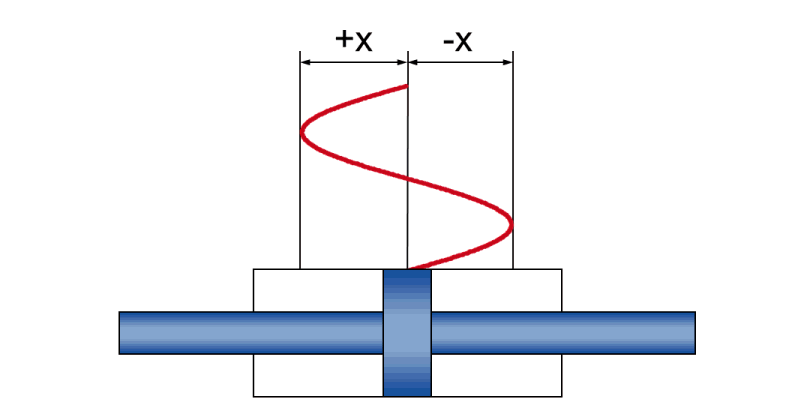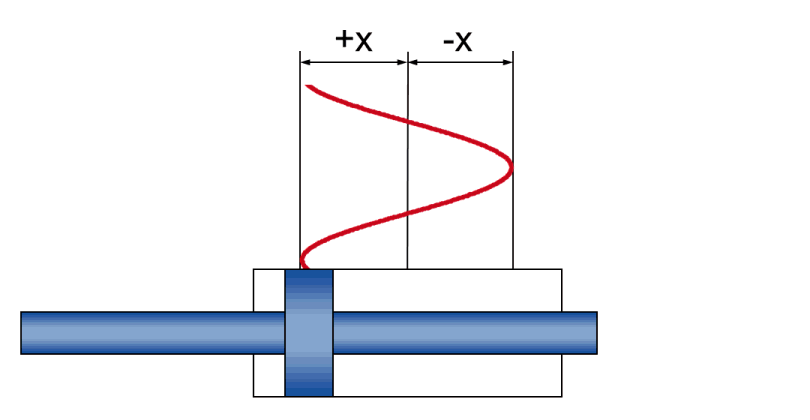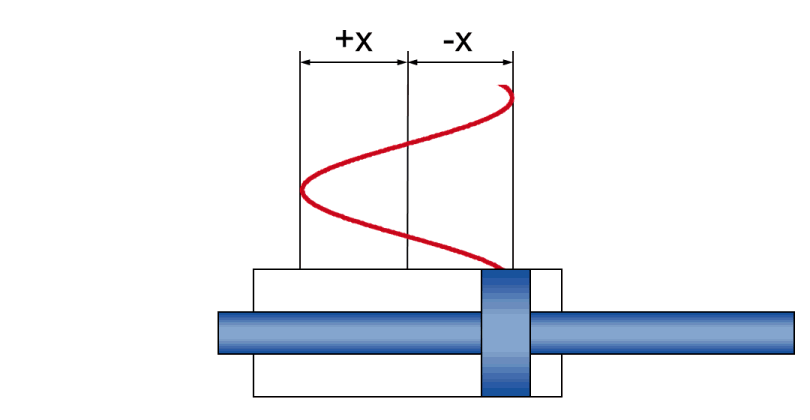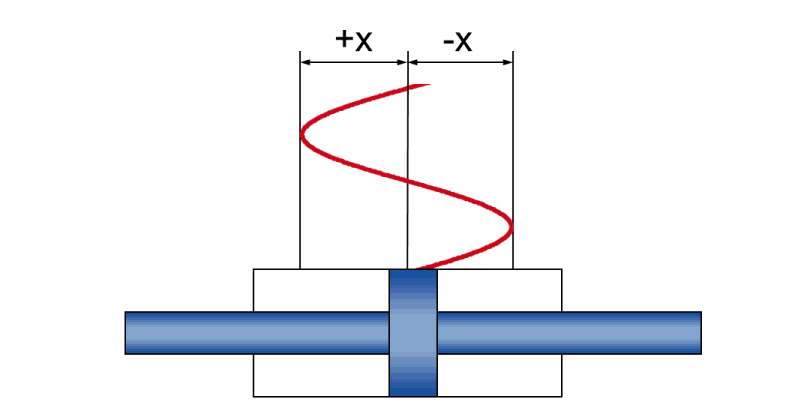
Movimiento sinusoidal dinámico
En el funcionamiento dinámico, un movimiento sinusoidal genera relaciones físicas entre
- Amplitud +/- x: el movimiento de la carrera real durante la oscilación
- Velocidad v: la velocidad del émbolo instantánea (y que cambia constantemente durante la oscilación)
- Aceleración a: la aceleración momentánea del pistón (que cambia constantemente durante la oscilación)
- Frecuencia f: la secuencia temporal del movimiento de la carrera, indicada como el número de oscilaciones por unidad de tiempo
| Valores máximos |
| v = 2 π f x |
| a = 4 π2 f2 x |
De esto resulta el caudal Q máximo requerido para el movimiento
Q = v • A
con la superficie efectiva del pistón A
A = π / 4 • (D2Pistón - d2Vástago)
y la fuerza de aceleración Fa que debe proporcionar el cilindro
Fa = m • a
A partir de la aceleración máxima calculada aquí y de la masa en movimiento, se obtiene una fuerza de aceleración que debe aplicar el cilindro. La masa propia del vástago se tiene en cuenta en el programa de cálculo; las masas en movimiento adicionales deben indicarse en el campo correspondiente.
Recomendación de la servoválvula
La presión del sistema ps se calcula teniendo en cuenta la caída de presión Δp en la válvula de regulación, válvula porporcional:
pb = ps - Δp
La caída de presión de la válvula de regulación, válvula porporcional se indica normalmente con 70 bar o 10 bar con caudal nominal en las válvulas de regulación. Sin embargo, en el funcionamiento, esto depende del caudal real.
El programa, en función del caudal requerido, propone un caudal nominal para una posible válvula de regulación, válvula porporcional. A continuación, también se calcula la caída de presión. El objetivo es obtener rápidamente una visión general de la clase de tamaño de válvula que sería necesaria.
Al valor de caudal calculado debe añadirse el caudal de aceite de fuga del sistema de sellado y de la servoválvula.
Esta configuración no afecta a la determinación y el diseño precisos de la válvula.
Otras fórmulas de cálculo para el diseño de cilindros hidráulicos:
Fórmulas de cálculo para el diseño de cilindros hidráulicos
Cálculo de las velocidades de aceite permitidas
Cálculo de la resistencia al pandeo de los cilindros hidráulicos
Cálculo de casos de pandeo: fijaciones del vástago y del cilindro